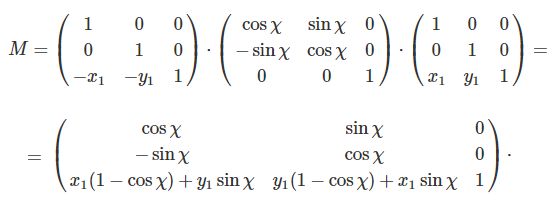Для описания произвольного перемещения фигуры на плоскости необходимо рассмотреть несколько простейших движений, таких как параллельный перенос, поворот относительно оси и зеркальное отражение относительно оси и точки (полюса), потому что любое сложное движение всегда можно представить как совокупность простых движений.

Параллельный перенос
Параллельный перенос на вектор переносит точку $M(x,y)$ в точку $M'(x',y')$. При этом координаты точек будут изменяться на величину проекции вектора параллельного переноса на соответствующую ось

$$x' = x + a_x\\
y' = y + a_y$$

При параллельном переносе отрезок перемещается параллельно самому себе, его длина и ориентация не изменяется (рис.1).

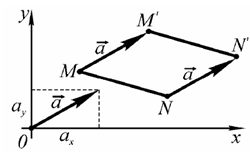
Рис.1. Параллельный перенос

Поворот
Поворот точки вокруг координатной оси против часовой стрелки на угол $χ$ (рис. 2а) изменяет координаты точки таким образом, что расстояние от точки до начала координат не изменяется:
$$x′ = x \cosχ − y \sinχ\\
y′ = x \sinχ + y \cosχ$$

При повороте отрезок не изменяет своей длины, а также не изменяются углы между совместно поворачиваемыми отрезками (рис. 2а).
Если необходимо выполнить поворот относительно произвольной точки, не совпадающей с началом координат, то сначала выполняется параллельный перенос полюса и поворачиваемого объекта на вектор $\overline{a}$, при котором полюс совпадет с началом координат. Затем выполняется поворот, а затем параллельный перенос на вектор ($-\overline{a}$ ) (рис. 2б).

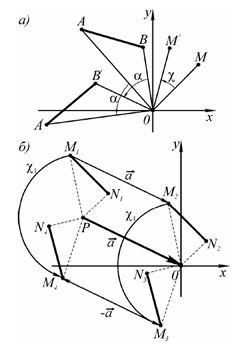
Рис.2. Поворот точки и отрезка

Отражение
Зеркальное отражение относительно оси абсцисс (рис. 3) приведет к тому, что координата x точки не меняется, а координата y меняет знак на противоположный

$$x' = x\\
y' = - y$$

При отражении относительно оси ординат знак меняется $у$ координаты $x$ , а у координаты $y$ знак не изменяется

$$x' = - x\\
y' = y$$

Отражение относительно начала координат изменяет знаки на противоположные у обеих координат:

$$x' = - x\\
y' = - y$$

В том случае, если отражение производится относительно произвольной оси, то до выполнения отражения необходимо будет выполнить параллельный перенос объекта и оси на вектор $\overline{a}$ так, чтобы ось отражения совпала с одной из координатных осей, затем выполнить отражение, а после этого выполнить параллельный перенос на вектор ($-\overline{a}$).
При отражении относительно произвольного полюса вначале выполняется параллельный перенос, совмещающий полюс с началом координат, затем отражение относительно начала координат и после этого параллельный перенос для возврата полюса в первоначальное положение.

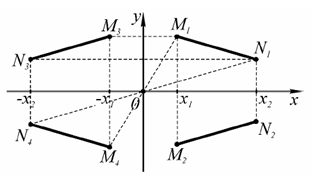
Рис.3. Отражение относительно оси и полюса.

Масштабирование и деформация
Кроме перемещений объекта по поверхности его можно деформировать. В случае если деформация будет пропорциональной, то ее можно рассматривать как масштабирование объекта. При деформации объекта координаты его точек изменяются на некоторую константу

$$x'= \alpha x\\
y' = \beta y$$

$\alpha$ и $\beta$ - коэффициенты масштабирования по осям абсцисс и ординат, соответственно. Если $\alpha = \beta$, то деформация будет пропорциональной (масштабирование (рис.4)). Если константы $\alpha$ и $\beta$ будут положительными, то производится только деформация, а если отрицательными, то кроме деформации происходит еще и отражение.

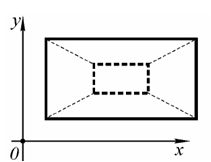
Рис.4. Масштабирование прямоугольника

Матричные преобразования

Для эффективного использования этих известных формул в задачах компьютерной графики более удобной является их матричная запись.

Определим точку следующим образом:$Р=(х,у)$ - начальная точка, $Р'=(х',у')$ - точка после преобразования.

Тогда матрица масштабирования и деформации:

$$
S=\begin{pmatrix}
\alpha & 0 \\
0 & \beta\\
\end{pmatrix} $$

а операция преобразования выглядит следующим образом:

$$P' = P\cdot S$$

Матрица поворота:

$$
R=\begin{pmatrix}
\cos χ & \sin χ \\
-\sin χ & \cos χ\\
\end{pmatrix} $$
соответственно преобразование поворота в матричном виде:
$$P' = P\cdot R$$

Матрица отражения относительно осей OX, OY:
$$
M_x=\begin{pmatrix}
1 & 0 \\
0 & -1\\
\end{pmatrix} ,
M_y=\begin{pmatrix}
-1 & 0 \\
0 & 1\\
\end{pmatrix}
$$
и соответствующие преобразования:
$$P' = P\cdot M_x, P' = P\cdot M_y$$

Все преобразования реализуются умножением матриц и лишь параллельный перенос выполняется как сложение:

$$ (x', y') = (x, y) + (dx, dy)$$

Однородные координаты

Чтобы реализовать все элементарные преобразования одним действием - умножением матриц, в геометрии вводится понятие однородных координат. Точка $Р(х, у)$ записывается как $P(Wx, Wy, W)$, где W - некоторый масштабный множитель и для простоты чаще всего принимается за 1.

Используя однородные координаты можно любое элементарное преобразование, описанное выше, задать как умножение матриц:
$$ P'=P\cdot M,$$
где $M$ - матрица элементарного преобразования или их произведения.

Таким образом матрица параллельного переноса имеет вид:
$$
D = \begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
Dx & Dy & 1 \\
\end{pmatrix}
$$

Матрица поворота:
$$
R = \begin{pmatrix}
\cos χ & \sin χ & 0\\
-\sin χ & \cos χ & 0\\
0 & 0 & 1 \\
\end{pmatrix}
$$

Матрица масштабирования и деформации:
$$
S = \begin{pmatrix}
\alpha & 0 & 0\\
0 & \beta & 0\\
0 & 0 & 1 \\
\end{pmatrix}
$$

Если $\alpha= \beta$, то масштабирование однородное с сохранением пропорций фигуры. Если $\alpha\neq \beta$, то происходит искажение пропорций фигуры по осям.

Матрица отражения по оси X:
$$
M_x = \begin{pmatrix}
-1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1 \\
\end{pmatrix}
$$

Матрица отражения по оси Y:
$$
M_y = \begin{pmatrix}
1 & 0 & 0\\
0 & -1 & 0\\
0 & 0 & 1 \\
\end{pmatrix}
$$

Используя однородные координаты можно эффективно применить к точке одно совмещенное преобразование (одно умножение на матрицу), чем ряд преобразований друг за другом. Например, поворот объекта относительно некоторой произвольной точки $P(x_1,y_1)$ выполняется 3 элементарными преобразованиями:

1. Перенос, при котором точка $P(x_1,y_1)$ помещается в начало координат;
2. Поворот;
3. Перенос в первоначальное положение.

А в матричном виде с однородными координатами, поворот относительно некоторой точки осуществляется одной результирующей матрицей: