Эта фигура — один из первых исследованных учеными фракталов. Она получается из трех копий кривой Коха, которая впервые появилась в статье шведского математика Хельге фон Коха в 1904 году. Эта кривая была придумана как пример непрерывной линии, к которой нельзя провести касательную ни в одной точке. Линии с таким свойством были известны и раньше (Карл Вейерштрасс построил свой пример еще в 1872 году), но кривая Коха замечательна простотой своей конструкции. Не случайно его статья называется «О непрерывной кривой без касательных, которая возникает из элементарной геометрии».

Как по шагам строится кривая Коха

Процесс её построения выглядит следующим образом: берём единичный отрезок, разделяем на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырёх звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т. д. Продолжая в том же духе, можно получать всё новые и новые линии (все они будут ломаными). А то, что получится в пределе (это уже будет воображаемый объект), и называется кривой Коха.

Основные свойства кривой Коха

• Кривая Коха нигде не дифференцируема и не спрямляема.
• Кривая Коха имеет бесконечную длину.
• Кривая Коха не имеет самопересечений.
• Фрактальная размерность равна log4/log3 = log₃4 ≈ 1,261859...

Демонстрационный ролик получения снежинки Коха

Снежинка Коха получается из равностороннего треугольника для каждой стороны которого применили алгоритм получения кривой Коха.

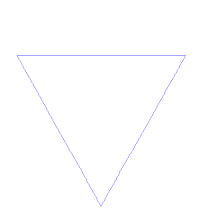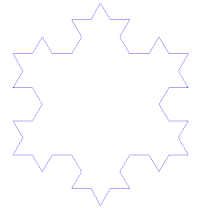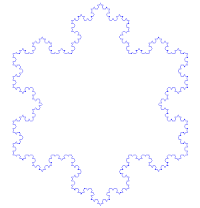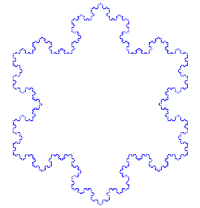
Варианты построения снежинки Коха

Рис.1. Снежинка Коха «наоборот» получается, если строить кривые Коха внутрь исходного равностороннего треугольника.

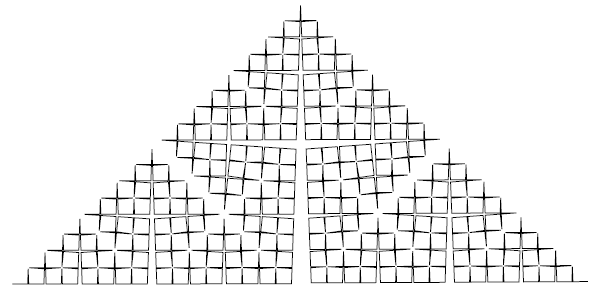
Рис.2. Линии Чезаро. Вместо равносторонних треугольников используются равнобедренные с углом при основании от 60° до 90°. На рисунке угол равен 88°.

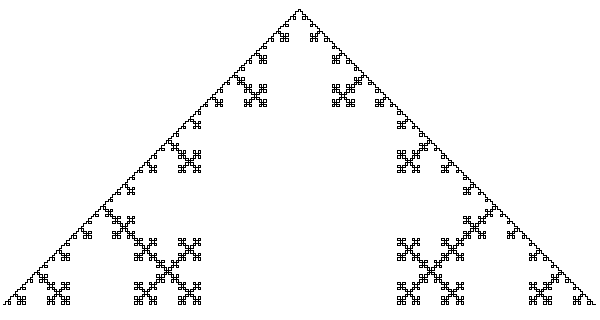
Рис.3. Квадратный вариант. Тут достраиваются квадраты.

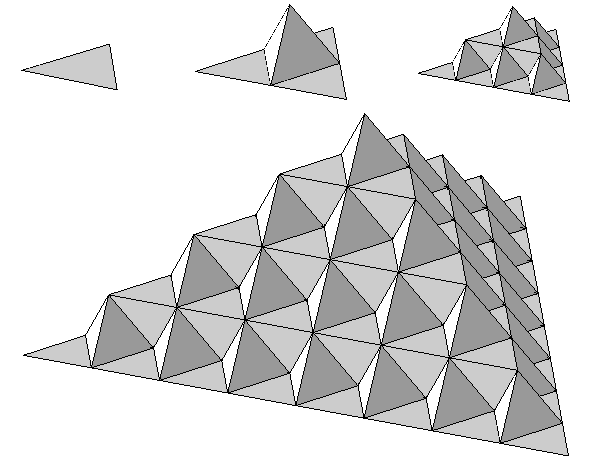
Рис.4. Трехмерные аналоги. Пирамида Коха