Кривые Безье — типы кривых, предложенные в 60-х годах XX века независимо друг от друга Пьером Безье из автомобилестроительной компании «Рено» и Полем де Кастельжо из компании «Ситроен», где применялись для проектирования кузовов автомобилей.

Несмотря на то, что открытие де Кастельжо было сделано несколько ранее Безье (1959), его исследования не публиковались и скрывались компанией как производственная тайна до конца 1960-х.

Впервые кривые были представлены широкой публике в 1962 году французским инженером Пьером Безье, который, разработав их независимо от де Кастельжо, использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастельжо назван разработанный им рекурсивный способ определения кривых (алгоритм де Кастельжо).

Благодаря простоте задания и манипуляции кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки опорных точек, то не пересекаются и сами кривые), а с другой стороны позволяет осуществлять интуитивно понятное управление параметрами кривой в графическом интерфейсе с помощью её опорных точек. Кроме того, аффинные преобразования кривой (перенос, масштабирование, вращение и др.) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.

Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, три смежные опорные точки обеих кривых должны лежать на одной прямой.

Виды кривых Безье

Линейные кривые

При n = 1 кривая представляет собой отрезок прямой линии, опорные точки $P_0(x_0,y_0)$ и $P_1(x_1,y_1)$ определяют его начало и конец.

Кривая задаётся уравнением:

$$x(t) = (1-t)x_0 + tx_1\\
y(t) = (1-t)y_0 + ty_1,
$$
где $t \in [0,1]$

Квадратичные кривые

Квадратичная кривая Безье (n = 2) задаётся тремя опорными точками: $P_0(x_0,y_0), P_1(x_1,y_1)$ и $P_2(x_2,y_2)$.

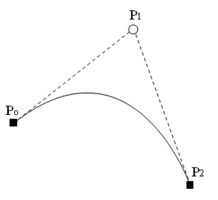
Параметрическое уравнение кривой:
$$x(t) = (1−t)^2x_0 + 2t(1−t)x_1 + t^2x_2\\
y(t) = (1−t)^2y_0 + 2t(1−t)y_1 + t^2y_2,$$
где $t \in [0,1]$

Кубические кривые
Четыре опорные точки $P_0(x_0, y_0), P_1(x_1, y_1), P_2(x_2, y_2)$ и $P_3(x_3, y_3)$, заданные в 2-х или 3-мерном пространстве, определяют форму кривой.

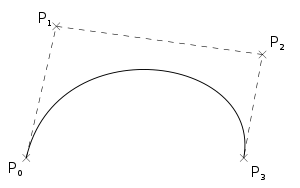
В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:

$$x(t) = (1−t)^3x_0 + 3t(1−t)^2x_1 +3t^2(1−t)x_2 + t^3x_3\\
y(t) = (1−t)^3y_0 + 3t(1−t)^2y_1 +3t^2(1−t)y_2 + t^3y_3,
$$
где $t \in [0,1]$

Алгоритм де Кастельжо построения кривых

Метод де Кастельжо идентичен математическому определению кривой и наглядно показывает, как она строится.

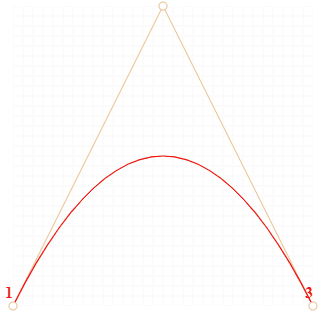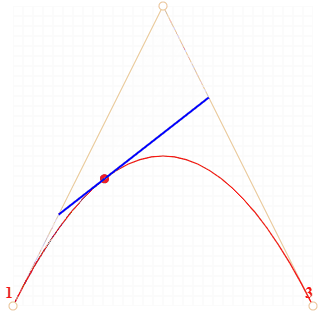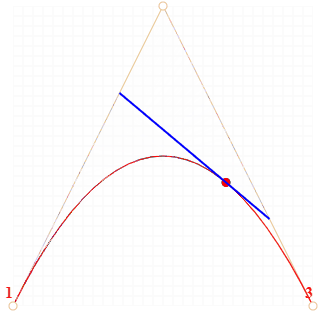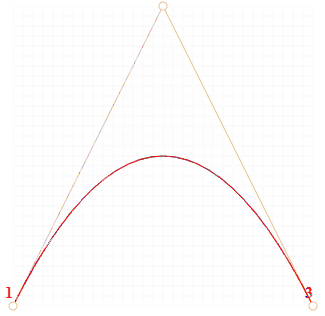
Рис.1. Алгоритм построения квадратичной кривой по методу Кастельжо.

Алгоритм построения кривой для трех точек:

1. Рисуем опорные точки. На рисунке 1 это точки 1, 2, 3.
2. Строятся отрезки между опорными точками 1 → 2 → 3. На рисунке 1 они коричневые.
3. Параметр t пробегает значения от 0 до 1. В примере использован шаг 0.05, т.е. в цикле 0, 0.05, 0.1, 0.15, ... 0.95, 1.

Для каждого из этих значений t:

• На каждом из коричневых отрезков берётся точка, находящаяся на расстоянии, пропорциональном t, от его начала. Так как отрезков два, то и точек две.
• Например, при t=0 – точки будут в начале, при t=0.25 – на расстоянии в 25% от начала отрезка, при t=0.5 – 50% (на середине), при t=1 – в конце отрезков.
• Эти точки соединяются. На рисунке ниже соединяющий их отрезок изображён синим.

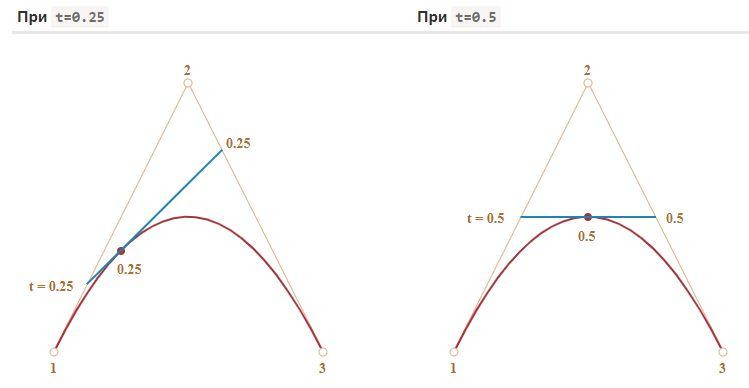
4. На получившемся синем отрезке берётся точка на расстоянии, соответствующем t. То есть, для t=0.25 (левый рисунок) получаем точку в конце первой четверти отрезка, для t=0.5 (правый рисунок) – в середине отрезка. На рисунках выше эта точка отмечена красным.
5. По мере того, как t «пробегает» последовательность от 0 до 1, каждое значение t добавляет к кривой точку. Совокупность таких точек для всех значений образует кривую Безье. Она красная и имеет параболическую форму на картинках выше.

Аналогично и с четырьмя точками.

Алгоритм построения кривой для четырех точек:

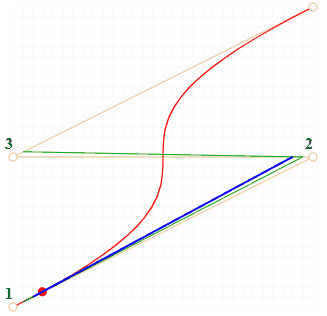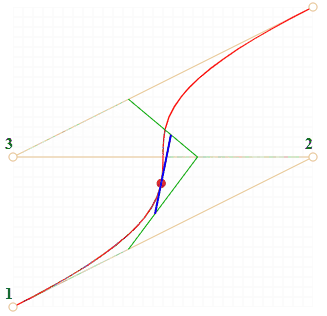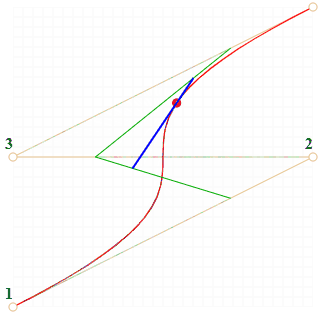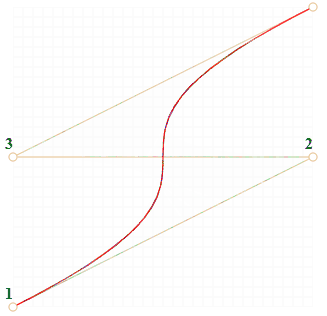
Точки по порядку соединяются отрезками: 1 → 2, 2 → 3, 3 → 4. Получается три коричневых отрезка.

Для t на отрезке от 0 до 1:

1. На отрезках берутся точки, соответствующие текущему t, соединяются. Получается два зелёных отрезка .
2. На этих отрезках берутся точки, соответствующие текущему t, соединяются. Получается один синий отрезок.
3. На синем отрезке берётся точка, соответствующая текущему t. При запуске примера выше она красная.
4. Эти точки вместе описывают кривую.

Алгоритм является рекурсивным и может быть обобщён на любое количество контрольных точек.

Рекурсивный алгоритм построения кривой для любого числа точек:

Дано N контрольных точек:

1. Соединяем их, чтобы получить N-1 отрезков.
2. Затем для каждого t от 0 до 1 берём точку на каждом отрезке на расстоянии пропорциональном t и соединяем их. Там будет N-2 отрезков.
3. Повторяем 2 шаг, пока не останется одна точка.
4. Эти точки образуют кривую.

Свойства кривой Безье

• непрерывность заполнения сегмента между начальной и конечной точками;
• кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки;
• при наличии только двух контрольных точек сегмент представляет собой прямую линию;
• прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек;
• кривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой;
• масштабирование и изменение пропорций кривой Безье не нарушает её стабильности, поскольку с математической точки зрения она «аффинно инвариантна»;
• изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье;
• любой частичный отрезок кривой Безье также является кривой Безье;
• степень (порядок) кривой всегда на одну ступень меньше числа контрольных точек. Например, при трёх контрольных точках форма кривой — парабола, так как парабола — кривая 2-го порядка;
• окружность не может быть описана параметрическим уравнением кривой Безье.