Алгоритм плавающего горизонта чаще всего используется для удаления невидимых линий трехмерного представления функций, описывающих поверхность в виде

$$F(x, y, z) = 0$$

Подобные функции возникают во многих приложениях в математике, технике, естественных науках и других дисциплинах.

Алгоритм работает в пространстве изображения. Главная идея метода заключается в сведении трехмерной задачи к двумерной путем пересечения исходной поверхности последовательностью параллельных секущих плоскостей, имеющих постоянные значения координат x, y или z.

На рис. 1 приведен пример, где указанные параллельные плоскости определяются постоянными значениями z. Функция $F(x, y, z) = 0$ сводится к последовательности кривых, лежащих в каждой из этих параллельных плоскостей, например к последовательности $y = f(x, z)$ или $x = g(y, z)$, где z постоянно на каждой из заданных параллельных плоскостей.

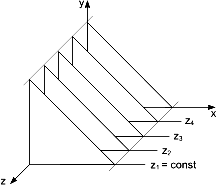
Рис.1. Параллельные плоскости определяются значениями z

Итак, поверхность теперь складывается из последовательности кривых, лежащих в каждой из этих плоскостей, как показано на рис. 2.

Рис.2. Последовательность кривых, лежащих в каждой из плоскостей z

Если спроецировать полученные кривые на плоскость $z = 0$, как показано на рис. 3, то становится ясна идея алгоритма удаления невидимых участков исходной поверхности.

Алгоритм сначала упорядочивает плоскости z = const по возрастанию расстояния от них до точки наблюдения. Затем для каждой плоскости, начиная с ближайшей к точке наблюдения, строится кривая, лежащая на ней, то есть для каждого значения координаты x в пространстве изображения определяется соответствующее значение y. Алгоритм удаления невидимой линии заключается в следующем: если на текущей плоскости при некотором заданном значении x соответствующее значение y на кривой больше значения y для всех предыдущих кривых при этом значении x, то текущая кривая видима в этой точке; в противном случае она невидима.

Рис.3. Результирующая проекция всех кривых на картинную плоскость z=0

Невидимые участки показаны пунктиром на рис.3. Реализация данного алгоритма достаточно проста. Для хранения максимальных значений y при каждом значении x используется массив, длина которого равна числу различимых точек (разрешению) по оси x в пространстве изображения. Значения, хранящиеся в этом массиве, представляют собой текущие значения «горизонта». Поэтому по мере рисования каждой очередной кривой этот горизонт «всплывает». На рис.4. красной линией показана кривая "плавающего горизонта" для шага z=5. Фактически этот алгоритм удаления невидимых линий работает каждый раз с одной линией.

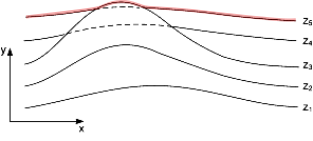
Рис. 4. Линия "плавающего горизонта"

Алгоритм работает очень хорошо до тех пор, пока какая-нибудь очередная кривая не окажется ниже самой первой из кривых, как показано на рис. 4.

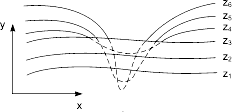
Рис.4. Выход кривой за нижний горизонт

Подобные кривые, естественно, видимы и представляют собой нижнюю сторону исходной поверхности, однако алгоритм будет считать их невидимыми. Нижняя сторона поверхности делается видимой, если модифицировать этот алгоритм, включив в него нижний горизонт, который опускается вниз по ходу работы алгоритма. Это реализуется при помощи второго массива, длина которого равна числу различимых точек по оси x в пространстве изображения. Этот массив содержит наименьшие значения y для каждого значения x. Алгоритм теперь становится таким: если на текущей плоскости при некотором заданном значении x соответствующее значение y на кривой больше максимума или меньше минимума по y для всех предыдущих кривых при этом x, то текущая кривая видима. В противном случае она невидима.

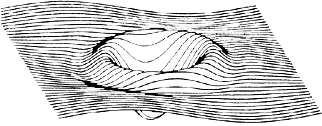
Рис.5. Типичный результат работы алгоритма плавающего горизонта.