Аполлониево множество — увлекательная математическая конструкция, демонстрирующая замысловатые узоры и свойства. Он назван в честь древнегреческого математика Аполлония Пергского, изучавшего круги и их свойства.

По своей сути аполлониево множество представляет собой фрактал, образованный серией касательных окружностей. Начиная с трех касательных окружностей, процесс построения включает рекурсивную установку меньших касательных окружностей в промежутки между существующими окружностями. Этот процесс можно продолжать бесконечно, в результате чего получится сложный и бесконечно детализированный узор.

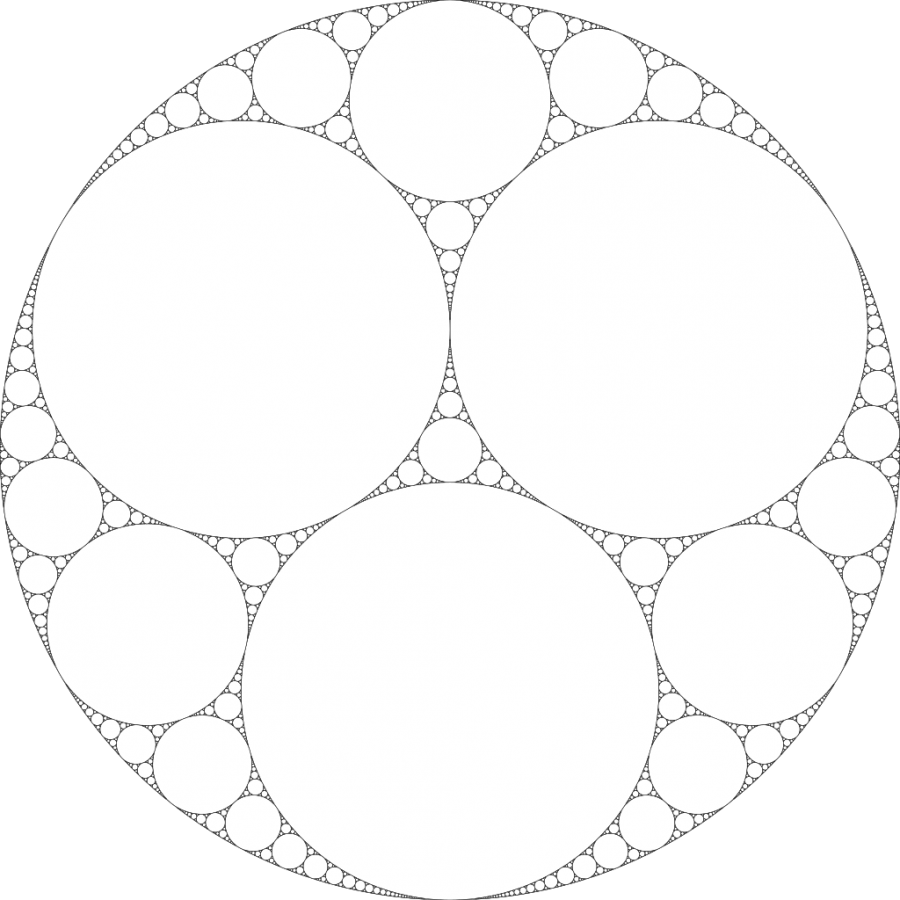
Аполлониево множество демонстрирует несколько интригующих характеристик.

• Во-первых, это фрактал, то есть он проявляет самоподобие в разных масштабах. Когда вы увеличиваете масштаб различных областей прокладки, вы обнаружите, что похожие узоры повторяются, хотя и в меньших размерах. Это свойство является одной из определяющих особенностей фракталов.
• Более того, аполлониево множество обладает замечательным свойством, известным как упаковка. Круги в прокладке плотно упакованы между собой без каких-либо зазоров и нахлестов. Это свойство тесно связано с концепцией упаковки кругов, областью изучения математики, изучающей расположение кругов в пространстве.
• Еще одним захватывающим аспектом аполлониевого множества является ее связь с теорией чисел. Кривизны кругов на множестве связаны с целыми числами, в частности с решениями некоторого диофанова уравнения. Эта связь между геометрическими свойствами кругов и теорией чисел добавляет прокладке более глубокий уровень математического значения.

Аполлониево множество привлекло внимание математиков, художников и энтузиастов благодаря своей сложной красоте и глубоким математическим свойствам. Он служит богатым источником исследований и вдохновения в таких областях, как фрактальная геометрия, упаковка кругов и теория чисел, демонстрируя глубокое взаимодействие между математикой и визуальной эстетикой.

Для построения Аполлониева множества требуется использовать алгоритм, известный как "метод инверсии".
Алгоритм:

1. Начните с трех взаимно касающихся окружностей. Эти окружности могут быть любого размера и расположены в любом положении, но они должны быть взаимно касающимися.
2. Найдите окружность, которая касается каждой из трех начальных окружностей. Это можно сделать с помощью операции инверсии.
3. Вставьте эту новую окружность в пространство между исходными окружностями. Она будет касаться каждой из них.
4. Повторите шаги 2 и 3 для новых окружностей, которые вы добавили, чтобы найти еще одну окружность, которая касается всех предыдущих окружностей.
5. Продолжайте повторять шаги 2, 3 и 4, добавляя все новые окружности, которые касаются предыдущих окружностей.

Процесс может быть продолжен бесконечно, и каждая новая окружность будет заполнять все более маленькие промежутки между существующими окружностями, создавая все более сложный и детализированный образец Аполлониева множества.